高级数据结构《算法基础-打开算法之门》

2022-07-30 | 阅读：次

高级数据结构

基础数据结构: 线性表(栈、队列、链表)，二叉树，图等

常见的数据结构, 堆排序是利用堆设计的选择排序

堆: 可以实现优先队列
树状结构: 区间和

Treap通过随机数优化二叉树, Splay树通过Splay操作维持平衡。左倾堆是一种可并堆,有左倾特性

堆

常见的数据类型—-二叉堆

堆的定义

堆是一棵完全的二叉树, 最重要的就是, 儿子不一定小于或者大于父亲的值(小堆顶, 大堆顶)

应用: 堆排列, 优先队列

利用数组存储的时候, 两个子节点的标号是, 2x+1, 2x+2

建堆

核心是调整堆, 满足没一个节点都不大于父节点的值, 从最后一个非叶子节点开始到根节点

堆排序的算法

设堆有n个元素, 每一次调整堆顶得到最大值, 然后将顶元素和最后一个元素互换, 对前n-1个元素调整直到有序

  1 #include <stdio.h>                                                                    
  2 void heap_adjust(int arr[], int father, int n)//数组, 起始位置, 数组的长度
  3 {   //传入一个堆栈, 从father位置开始,长度为n, 调整father位置的数值到正确的位置
  4     int child = father*2 + 1;
  5     int temp = arr[father];
  6     while(child < n){//当没有超出的时候
  7         if(child+1<n && arr[child]<arr[child+1])child++;
  8         if(arr[father]>=arr[child])break;//位置正确,大于子类的最大值, 退出
  9         arr[father]=arr[child];//交换
 10         father = child;//重新定位
 11         child = father*2+1;//调整位置
 12         arr[father] = temp;
 13     }
 14 }
 15 //数组,总共的元素
 16 void build_heap(int arr[], int n)
 17 {//建立堆区,把不是叶的节点全部调整一次
 18     for(int i=(n-1)/2;i>=0;--i)//从不是叶的节点的位置从下到上开始遍历
 19         heap_adjust(arr, i, n);
 20 }
 21 //数组,起始位置,结束位置
 22 void heap_sort(int arr[], int beg, int end)
 23 {
 24     build_heap(arr+beg, end - beg);//建立堆区
 25     for(int tmp, i= end-1; i>beg;--i)
 26     {
 27         tmp = arr[i];
 28         arr[i] = arr[0];
 29         arr[0] = tmp;//进行换位
 30         heap_adjust(arr+beg, 0, i);//对换上来的进行调整                                       
 31     }
 32 }
 33 int main(void){
 34     int arr[100];
 35     int n;
 36     scanf("%d", &n);
 37     for(int i=0; i<n;i++)
 38         scanf("%d", &arr[i]);//建立数组
 39     heap_sort(arr, 0, n);//排序
 40     for(int i = 0; i<n;++i)printf("%d ", arr[i]);
 41     return 0;
 42 }

树状数组

定义

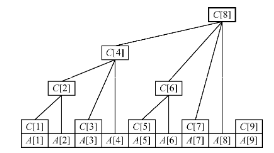
QQ图片20220801120149

给定一个数组, 更新某个点的值, 求某个区间的和, 对于普通的数组分别为O(1)和O(n), 对于树状数组,都为O(nlog n)

定义 \(C[i] = A[i-2^k +1] + ... + A[i]\) k为用二进制表示的时候末尾的0的个数, 也就是i是2^k的倍数

C[i]为A[i]开始前2^k项的和

求2^k的快捷方法

int lowbit(x){
    return x&(-x);
} //再求负数的时候, 所有的末尾的0变为1再加一,使得原本第一位不是的变为1, 有且只有这一位是政府同时1的

修改某一点的值的时候要修改他所有的父节点,它的父节点是 \(i+lowbit(i)\)

//在posion处加value,数组的长度是len
void change(int c[], int posion, int value, int len){
    while(posion <= len)
    {
        c[posion] += value;
        posion += lowbit(posion);
    }
}

前n项的和可以记为sum(n) \(sum(n) = C[n]+sum[n-lowbit(n)];\)

int sun(int c[], int n)
{
    int answer = 0;
    while(n>0)
    {
        answer += c[n];
        n -= lowbit(n);
    }
    return answer;
}

计算一个数列每次只能交换相邻的两个数据, 从小到大要使用的次数

建立一个树状数列, 在每添加一个数的时候, 在这个数列的对应位置置一, 然后对添加数的位置前面的数求和就是小于这个数的数字的数量, 所有的数字的逆序对相加就是结果

  1 #include <stdio.h>                                                                    
  2 #include <string.h>
  3 
  4 const int N = 1000;
  5 int lowbit(int x){
  6     return x&(-x);
  7 }
  8 
  9 void change(int c[], int posion, int value, int len){
 10     while(posion <= len)
 11     {
 12         c[posion] += value;
 13         posion += lowbit(posion);
 14     }
 15 }
 16 
 17 int sum(int c[], int n)
 18 {   
 19     int answer = 0;
 20     while(n>0)
 21     {
 22         answer += c[n];
 23         n -= lowbit(n);
 24     }
 25     return answer;
 26 }
 27 
 28 int main(void){
 29     int n;
 30     int c[N];
 31     while(~scanf("%d", &n))
 32     {
 33         memset(c, 0, sizeof(c));
 34         int x;
 35         int answer = 0;
 36         for(int i=1;i<=n;i++)
 37         {
 38             scanf("%d", &x);
 39             change(c, x, 1, n);
 40             answer += i -sum(c, x);
 41         }
 42         printf("%d\n", answer);
 43         printf("------\n");
 44     }
 45     return 0;
 46 }

左倾堆

实现两个堆的合并

XuSenfeng